Gekreuzte Vierecke können so arrangiert werden, daß dreidimensionale Gebilde entstehen, die wie Kronen aussehen. Diese werden folglich "Kronenpolyeder" genannt. Ihre Konstruktion gelingt, wenn man Prismen oder Anriprismen zugrunde legt, deren Ecken man mit den Seiten der gekreuzten Vierecke verbindet. Kronenpolyeder haben Rotationssymmetrie, die von der des zugrundeliegenden Prismas abgeleitet wird. Hier einige Beispiele:
In uniformen Polyedern sind die Vielecke bis auf wenige Ausnahmen immer paarweise auf parallelen Ebenen angeordnet. Solche Paare kann man als Grundflächen von Prismen oder Antiprismen betrachten, mit deren Ecken folglich Kronenpolyeder konstruiert werden können. Läßt man dann die Symmetrieelemente des uniformen Polyeders darauf einwirken, so entstehen ganz neue Gebilde, die aus gekreuzten Vierecken bestehen, und die dieselbe Symmetrie haben wie das ursprüngliche uniforme Polyeder.
Diese neuen Körper sind meist Zusammensetzungen ("compounds") von n Kronenpolyedern, wenn n gleich der Anzahl der Paare paralleler Vielecke derselben Art ist, von der das Kronenpolyeder abgeleitet wurde. Allerdings finden sich auch viele wunderschöne neue Einzelpolyeder mit sehr interessanten Eigenschaften. Unter ihnen sind viele Toroide, einige sind isoedrisch.
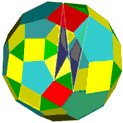
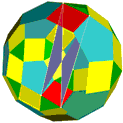
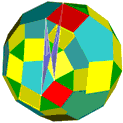
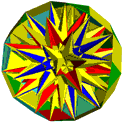
Die folgende Reihe von Abbildungen zeigt das Prinzip, nach dem die neuen Modelle erhalten werden.
Die folgende Galerie zeigt einige Beispiele von Kronenpolyedern, die aus uniformen Poyedern konstruiert wurden. Alle Modelle wurden mit der Software Great Stella erzeugt. Die Galerie ist so aufgebaut, dass durch Klick auf ein kleines Bild eine Vergrößerung erscheint. Klickt man auf das große Bild, so ist ein VRML-Modell zugänglich, das mit einem entsprechenden Player (z.B. Cortona) betrachtet werden kann.
Viel Spaß!