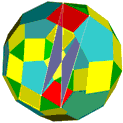
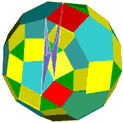
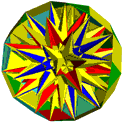
Crossed quadrilaterals can be arranged in a way, that 3-dimensional figures result which look like crowns. These are called crown polyhedra. Their construction is possible, if you take prisms or antiprisms as a basis, the vertices of which are connected by the edges of the crossed quadrilaterals. Crown polyhedra have rotational symmetry, depending from that of the basic prism. Here are some examples:
In uniform polyhedra the polygons are (with a few exceptions) always arranged in pairs on parallel planes. Such pairs can be taken for basic faces of prisms or antiprisms, with the vertices of which crown polyhedra can be constructed. If you apply the symmetry elements of the uniform polyhedron afterwards, completely new bodies result, which consist of crossed quadrilaterals and which have the same symmetry like the basic uniform polyhedron.
Mostly, these new shapes are compounds of n crown polyhedra if n is equal the number of pairs of polygons of the same kind, from which the crown polyhedron has been created. On the other hand, many beautiful and interesting new singular polyhedra appear. Many of them are toroids, some are isohedral.
The following series of pictures shows the principle how the new models are available.
The following gallery shows some examples of crown polyhedra which were created from uniform polyhedra. All models were created with the software "Great Stella". The gallery is organized in that way that a click on a thumbnail opens an enlarged picture. If you click on the large picture, a VRML-model is available which can be handled with a player (e. g. the cortona player).
Have fun!